Copyright © 2009 MNF Lab. - All Rights reserved.
The ability to shrink regular laboratory operations down to a small microfluidic chip is very appealing. Compact devices reduce both the time of synthesis/analysis and the cost of reagent while allow samples to be analyzed at the point-of-need. Applying microfuid systems with free liquid-vapor or liquid-liquid interfaces, i.e., open microfuidic systems may provide various advantages. In these systems not only because of the presence of the free interfaces less energy is dissipated and clogging can be prevented but also because of inherent observability and direct accessibility of these systems one can conveniently insert/remove the liquid, follow the process and clean the surfaces after use. Open microfuidic devices can be constructed either by chemically or topographically patterning the substrates. Liquids on topographically patterning substrates exhibit a rich variety of wetting morphologies and can spread spontaneously along these substrates. While present devices are based mostly on micron sized channels, further miniaturization down to the nanoscale is clearly on the roadmap. This will eventually lead to nanofluidic systems for which a variety of physical phenomena, which on the microscale and above are either irrelevant or summarized into boundary conditions, become important. For the optimization of the performance of nanofluidic systems it is critical to understand the basic fluidic issues occurring on those scales. Most investigations have been concerned with equilibrium configurations and the corresponding dynamics has been much less understood on those scales. Recent studies of nanoscale fluids on topographically [1,2] or chemically [3-5] structured substrates have underscored the importance of such investigations.
[1] A. Moosavi, M. Rauscher, and S. Dietrich, Dynamics of nanodroplets near nanometric steps, Accepted for publication as a special issue article on dynamics of wetting , J. Phys. Condens. Matter, 2009.
[2] A. Moosavi, M. Rauscher, and S. Dietrich, Motion of nanodroplets near edges and wedges, Phys. Rev. Lett, 97, 236101 (2006).
[3] A. Moosavi, M. Rauscher, and S. Dietrich, Size dependent motion of nanodroplets on chemical steps, J. Chem. Phys. , 129, 044706 (2008).
[4] A. Moosavi, M. Rauscher, and S. Dietrich, Motion of nanodroplets near chemical heterogeneities, Langmuir, 24, 734 (2008).
[5] M. Cieplak, J. Koeplik, and J. R. Banavar, Phys. Rev. Lett. , 96, 114502 (2006).
Clearly further investigation on this topic is necessary. Some ongoing researches and future plans involve the following studies:
» The behavior of nanodroplets on chemically and topographically structured substrates will be further studied (theory, simulation, and possibly experiment). The researches in progress [6] include studying dynamics of nanodropelts over chemically patterned substrates.
[6] A. Moosavi, M. Rauscher, and S. Dietrich, Dynamics of nanodroplets on chemically patterned substrates, in progress.
»The effect of temperature (thermocapillary phenomena) / electrostatic forces, and other relevant issues on the dynamics of nanodroplets near and on structured substrates.
» Dewetting over nanostructured substrates. Recent experimental study [7] has revealed interesting feature for dewetting over nanometric steps. Some numerical simulations have been performed on this issue [2]. The results are encouraging.
[7] T. Ondarcuhu and A. Piednoir, Nano Lett., 5, 1744 (2005).
[8] A. Moosavi, M. Rauscher, and S. Dietrich, Dewetting on nanometric steps, in
progress.
» Condensation and Evaporation on the structured substrates will be studied at the nanoscale.
»The contact line dynamics on structured substrates. We plan to use Lattice Boltzmann method for this purpose.
[1] A. Moosavi, M. Rauscher, and S. Dietrich, Dynamics of nanodroplets near nanometric steps, Accepted for publication as a special issue article on dynamics of wetting , J. Phys. Condens. Matter, 2009.
[2] A. Moosavi, M. Rauscher, and S. Dietrich, Motion of nanodroplets near edges and wedges, Phys. Rev. Lett, 97, 236101 (2006).
[3] A. Moosavi, M. Rauscher, and S. Dietrich, Size dependent motion of nanodroplets on chemical steps, J. Chem. Phys. , 129, 044706 (2008).
[4] A. Moosavi, M. Rauscher, and S. Dietrich, Motion of nanodroplets near chemical heterogeneities, Langmuir, 24, 734 (2008).
[5] M. Cieplak, J. Koeplik, and J. R. Banavar, Phys. Rev. Lett. , 96, 114502 (2006).
Clearly further investigation on this topic is necessary. Some ongoing researches and future plans involve the following studies:
» The behavior of nanodroplets on chemically and topographically structured substrates will be further studied (theory, simulation, and possibly experiment). The researches in progress [6] include studying dynamics of nanodropelts over chemically patterned substrates.
[6] A. Moosavi, M. Rauscher, and S. Dietrich, Dynamics of nanodroplets on chemically patterned substrates, in progress.
»The effect of temperature (thermocapillary phenomena) / electrostatic forces, and other relevant issues on the dynamics of nanodroplets near and on structured substrates.
» Dewetting over nanostructured substrates. Recent experimental study [7] has revealed interesting feature for dewetting over nanometric steps. Some numerical simulations have been performed on this issue [2]. The results are encouraging.
[7] T. Ondarcuhu and A. Piednoir, Nano Lett., 5, 1744 (2005).
[8] A. Moosavi, M. Rauscher, and S. Dietrich, Dewetting on nanometric steps, in
progress.
» Condensation and Evaporation on the structured substrates will be studied at the nanoscale.
»The contact line dynamics on structured substrates. We plan to use Lattice Boltzmann method for this purpose.
(a) (b)
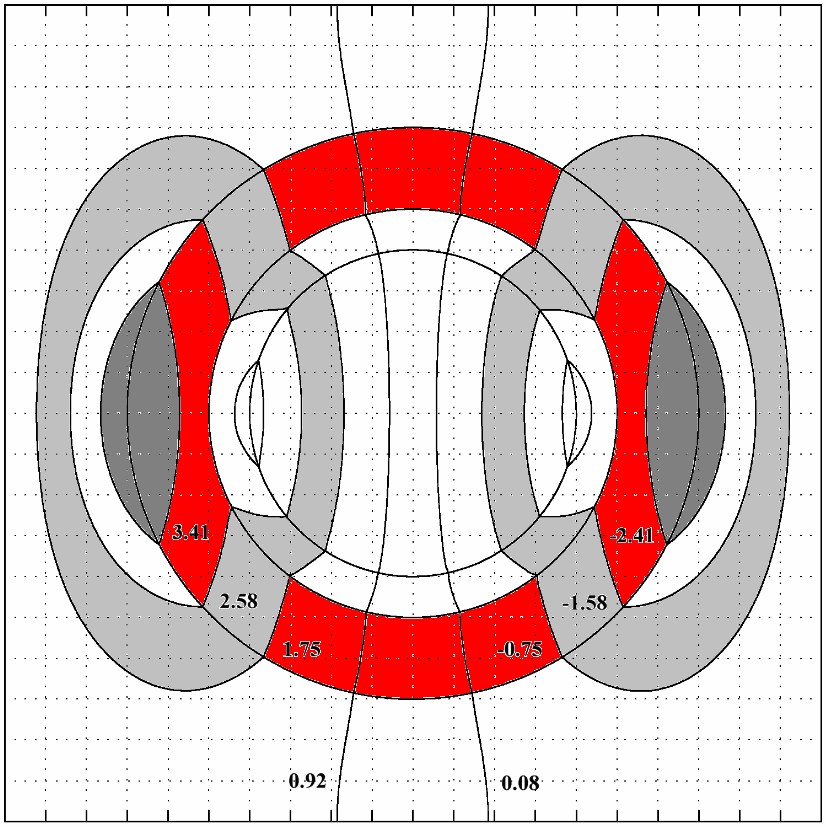
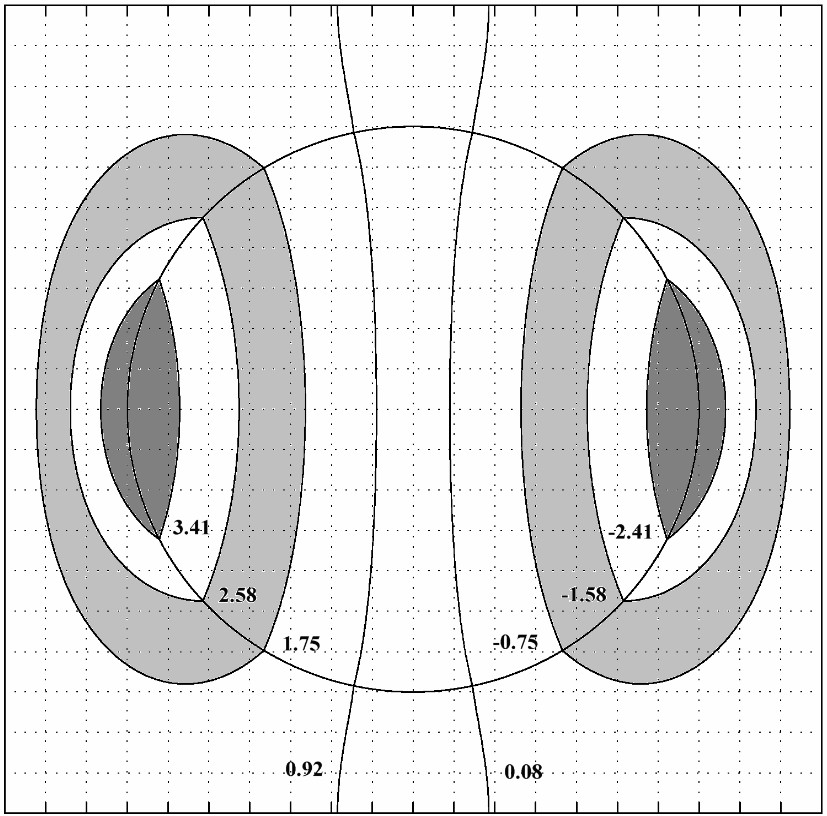
Figure 1. A three-phase partially resonant system (a) and the equivalent system (b).
[3] A. Moosavi, P. Sarkomaa, and W. Polashenski, The effective conductivity of
composite materials with cubic arrays of multi-coated spheres, Appl. Phys. A 77, 441
(2003).
[4] A. Moosavi, P. Sarkomaa, The resonant behavior of a multi-phase composite material, Int. J. Mod. Phys. C 13, 405 (2002).
»To a large extend the investigations performed in this field consider circular (spherical) inclusions in two phase systems. Extending the discussion to multi-phase and more realistic systems and performing the experimental investigation for the cases will be our main purpose in this section.
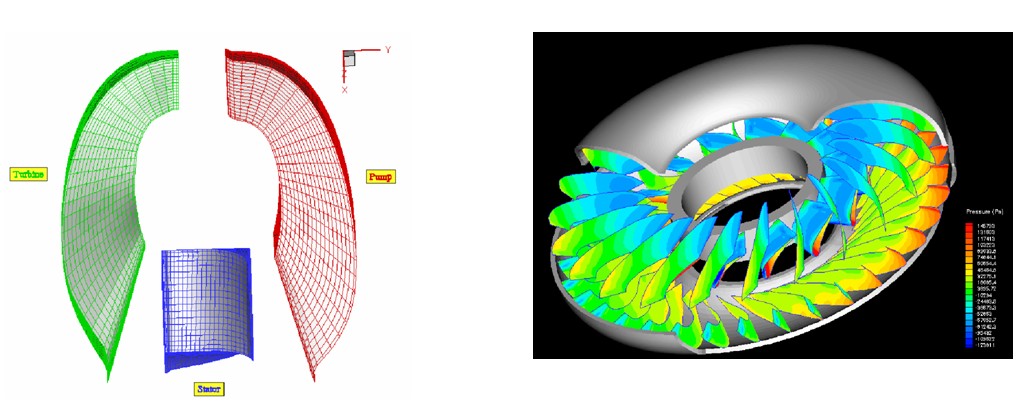
Figure 1. Grid Generation Figure 2. Contours of pressure
2) Simulation of the flow in packed beds with cylindricla and spherical particles via
Fluent 5 (TEKES project: Lappeenrant University of Technology).
Fluent 5 (TEKES project: Lappeenrant University of Technology).
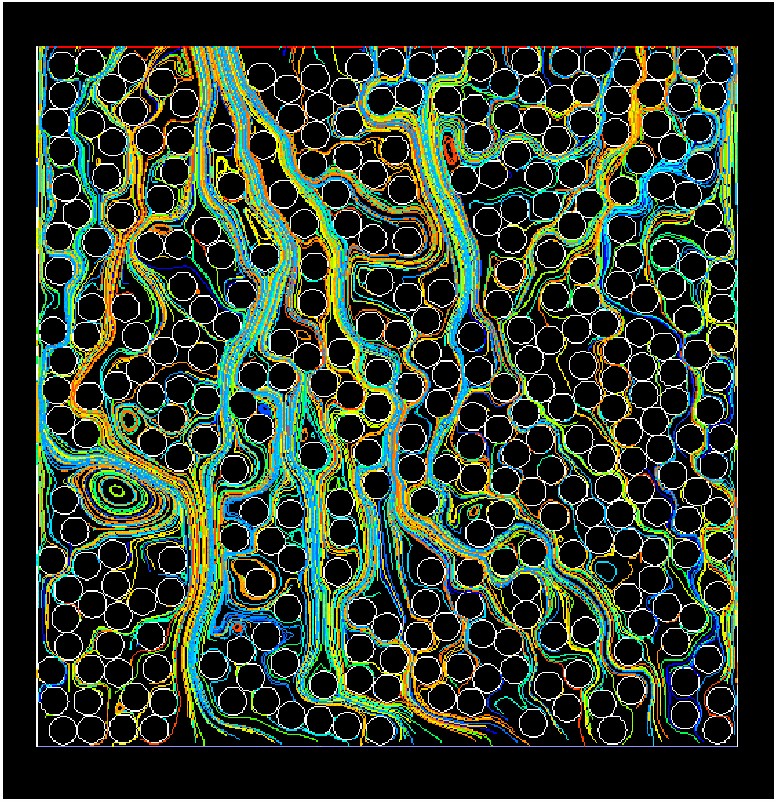
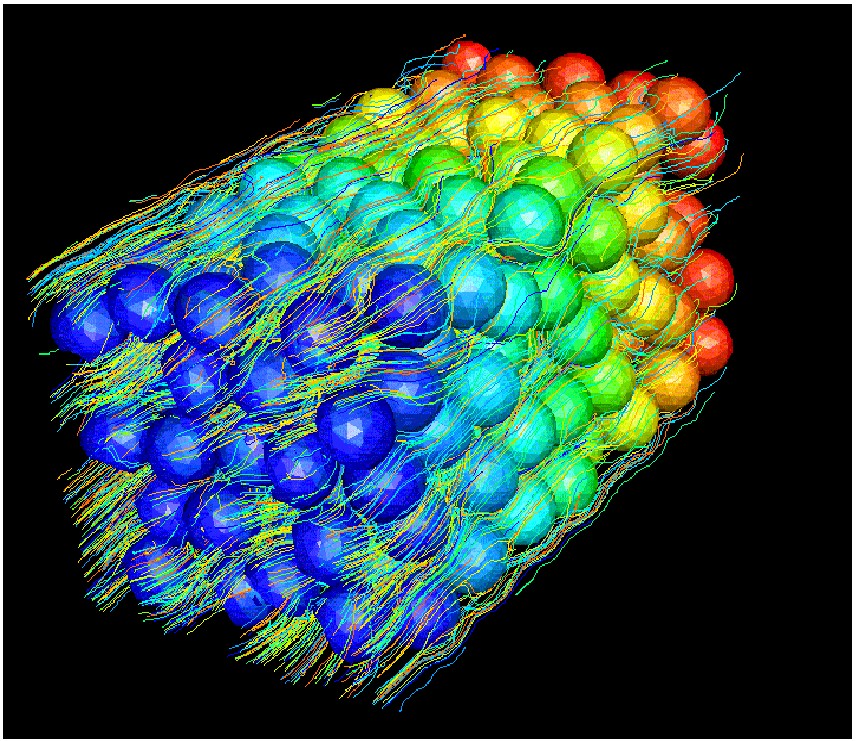
(a) (b)
Figure 3. Fluid flow in a packed bed (a) 2-D Modeling (b) 3-D modeling
Figure 3. Fluid flow in a packed bed (a) 2-D Modeling (b) 3-D modeling
3) Characterization of Carbonate sediments ( Statoil Project: University of Stuttgart)
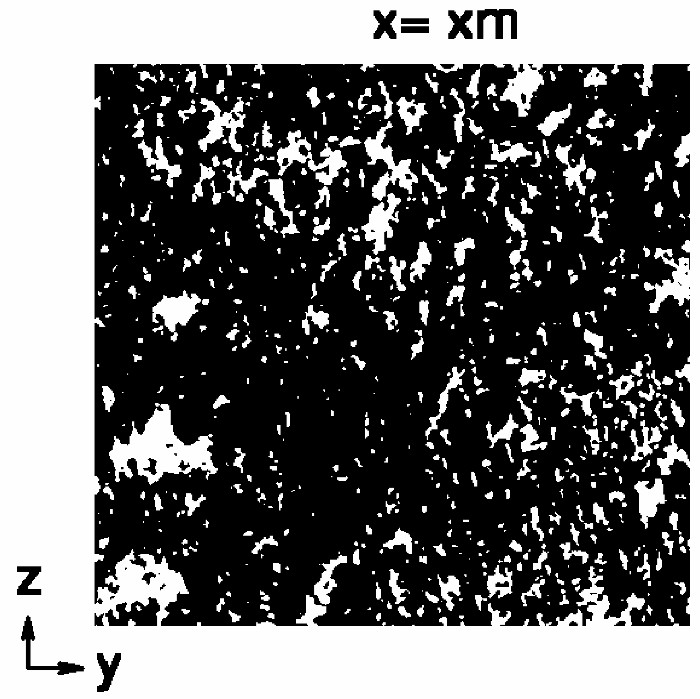
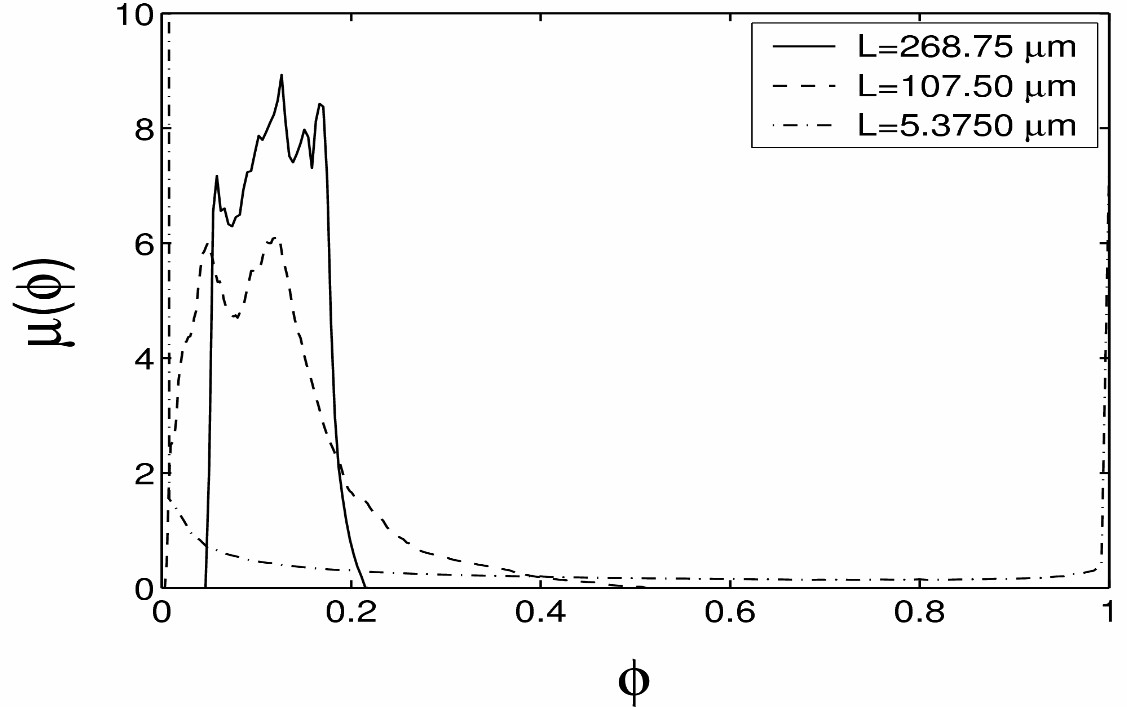
(a) (b)
Figure 4. The external surface of a carbonate sample (micro-CT image) (b) Local porosity distribution of the
sample
Figure 4. The external surface of a carbonate sample (micro-CT image) (b) Local porosity distribution of the
sample
Our second line of research involves calculating transport properties (conductivity, permeability,...) of multi- phase heterogenous systems based on their microstructure. Some works have already been done:
[1] A. Moosavi, P. Sarkomaa, Critical resistance for multi-phase composite materials, Phys. Lett. A 313, 218 (2003).
[2] A. Moosavi, P. Sarkomaa, The effective conductivity of three-phase composite materials with circular cylindrical inclusions, J. Phys. D 36, 1644 (2003).
[1] A. Moosavi, P. Sarkomaa, Critical resistance for multi-phase composite materials, Phys. Lett. A 313, 218 (2003).
[2] A. Moosavi, P. Sarkomaa, The effective conductivity of three-phase composite materials with circular cylindrical inclusions, J. Phys. D 36, 1644 (2003).
1) Turbomachinery project: Simulation of the flow inside an automotive torque converter (Pride CD-5) and deriving important information such as the characteristic and efficiency curves, stall point position, etc (Tarh Negasht Co.).